CodinGame: Best fit to data - Rust - Regression Analysis

We will discuss exercise:

Coding Games and Programming Challenges to Code Better

CodinGame is a challenge-based training platform for programmers where you can play with the hottest programming topics. Solve games, code AI bots, learn from your peers, have fun.

CodinGame

Goal is find best fitting model for given dataset. For example for data:

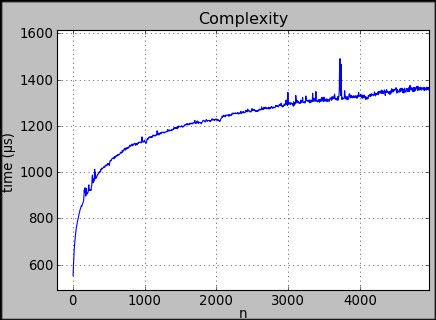
we should print O(log n). We can select models from list:

• O(1),
• O(log n),
• O(n),
• O(n log n),
• O(n^2),
• O(n^2 log n),
• O(n^3),
• O(2^n)

Input of program will contain first line with number of next lines and any following line will contain n and t values.

There are constrains:

5 < N < 1000
5 < num < 15000
0 < t < 10000000

and exemplary input:

10
5 341
1005 26324
2005 52585
3005 78877
4005 104925
4805 125920
6105 159156
7205 188017
8105 211417
9905 258991

should give to us

O(n)

because of is is similar to linear growth.

Least Square Fitting

We can derive equation on coefficient and assuming that we want to minimize sum of second powers of differences between measurement and prediction of our model.

This approach is called least squares fitting, and you can read more about it on MathWorld

Least Squares Fitting -- from Wolfram MathWorld

A mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets (“the residuals”) of the points from the curve. The sum of the squares of the offsets is used instead of the offset absolute values because this allows the residua…

from Wolfram MathWorld

Minimal value means that partial derivative by parameter of model a is 0.

Linear Regression

Now we can assume that function is linearly dependent from scaling parameter a.

Our goal is find equation to compute a and then R^2. Our derivative can be simplified:

Using last equation from Linear Square Fitting we can compute a

so

and

Our equations looks beautifully but the devil is in the details.

If we will look at constrains of data for this exercise:

5 < N < 1000
5 < num < 15000
0 < t < 10000000

and remember models that we need to test it is easy too see that we will operate on huge numbers.

For example 2^n with n = 15 000 is much more than max range of 64 bit float

MAX in std::f64 - Rust

Largest finite `f64` value. Use [`f64::MAX`] instead.

logo

that is constrained to 2^1024. There are tricks that allow to operate on these ranges, but instead of hacking computers constrains we will use math.

Instead of operating on big numbers we will use their logarithm to computation.

Logarithmic Regression

Our solution is consequence of observation that if we will match logarithms of models to logarithms of t data then in result will will select the same model.

So adding log both to data and function we getting equation:

rewriting this equation we can obtain a

where

and rewriting equation for R^2 we see:

Lets introduce new variable c defined as

and then R^2 can be rewritten as

we can see that now there is no chance to operate on too big numbers so we can start implementation of these equations.

Reading series of data from standard input

Lets start from definition of Point structure that represents single measurement.

#[derive(Debug)]
struct Point {
    n: u32,
    t: u32,
}

in main we will read standard input to String named buffer.

fn main() {
    let mut buffer = String::new();
    std::io::stdin().read_to_string(&mut buffer).unwrap();
}

we want to process this buffer and obtain vector of Points. To do it we writing function:

fn read_series(input: String) -> Vec<Point> {
    let mut iterator = input.lines();
    let n = iterator.next();
    let mut res: Vec<Point> = vec![];

    if Some(n).is_some() {
        for line in iterator {
            if let Some((n, y)) = line.split_once(' ') {
                res.push(Point {
                    n: n.parse::<u32>().unwrap_or(0),
                    t: y.parse::<u32>().unwrap_or(0),
                });
            }
        }
        return res;
    }

    return vec![];
}

we can check if it works adding to main line

    println!("{:?}", read_series(buffer));

Computing sum on series using closure

In presented equations we had some sums, so to simplify further code lets implement sum function that can use closures to define operation what should be summed.

I initially wrote it as noob

fn sum(series: &Vec<Point>, expression: impl Fn(&Point) -> f64) -> f64 {
    let mut res = 0f64;
    for point in series {
        res += expression(point)
    }
    res
}

but soon fixed as hacker

fn sum(series: &Vec<Point>, expression: impl Fn(&Point) -> f64) -> f64 {
    series.into_iter().fold(0f64, |acc, point| { acc + expression(point) })
}

we can add test

#[cfg(test)]
mod tests {
    use crate::{Point, sum};

    #[test]
    fn sum_test() {
        assert_eq!(sum(
            &vec![Point { n: 0u32, t: 1u32 }, Point { n: 1u32, t: 2u32 }],
            |p: &Point| { f64::from(p.t) },
        ), 3f64);
    }
}

Evaluating Sum of Least Squares

Our models to test can be represented using structure

struct Model {
    name: String,
    fn_log: fn(u32) -> f64,
}

but after computing R^2 we can save result as

struct EvaluatedMode {
    name: String,
    r2_log: f64,
}

this is convenient data organization because results of evaluation will be compared by r2_log but then name should be available to print as output.

Due to this reason we will select following signature for R^2 evaluation

fn evaluate_r2(model: Model, series: &Vec<Point>) -> EvaluatedMode

Series is passed by reference similarly like in sum. We do not want to change them or copy so operating on reference is preferred option for us.

Rewriting equations derived before to rust we can implement in this way

fn evaluate_r2(model: Model, series: &Vec<Point>) -> EvaluatedMode {
    let Model { name, fn_log } = model;
    let c = 1.0 / series.len() as f64 * sum(
        &series,
        |p| { f64::ln(f64::from(p.t)) - fn_log(p.n) },
    );
    let r2_log = sum(
        &series,
        |p| f64::powi(f64::ln(f64::from(p.t)) - fn_log(p.n) - c, 2),
    );
    EvaluatedMode {
        name,
        r2_log,
    }
}

Selection best fitting model

To select model we starting from function signature

fn select_model(series: &Vec<Point>) -> String {

and defining vector with models possible to select. Instead of original functions we adding fn_log what are logharithms of these functions.

    let models: Vec<Model> = vec![
        Model {
            name: String::from("O(1)"),
            fn_log: |_n| 0f64,
        },
        Model {
            name: String::from("O(log n)"),
            fn_log: |n| f64::ln(f64::ln(f64::from(n))),
        },
        Model {
            name: String::from("O(n)"),
            fn_log: |n| f64::ln(f64::from(n)),
        },
        Model {
            name: String::from("O(n log n)"),
            fn_log: |n| f64::ln(f64::from(n)) + f64::ln(f64::ln(f64::from(n))),
        },
        Model {
            name: String::from("O(n^2)"),
            fn_log: |n| 2.0 * f64::ln(f64::from(n)),
        },
        Model {
            name: String::from("O(n^2 log n)"),
            fn_log: |n| 2.0 * f64::ln(f64::from(n)) + f64::ln(f64::ln(f64::from(n))),
        },
        Model {
            name: String::from("O(n^3)"),
            fn_log: |n| 3.0 * f64::ln(f64::from(n)),
        },
        Model {
            name: String::from("O(2^n)"),
            fn_log: |n| f64::from(n) * f64::ln(2.0),
        },
    ];

finally we mapping these models to evaluated models and reducing result to model with smallest r2_log

    models.into_iter().map(|m| { evaluate_r2(m, series) }).reduce(|p, n| {
        if p.r2_log < n.r2_log { p } else { n }
    }).unwrap().name
}

its everything. Now we can change last line of main to

    println!("{}", select_model(&read_series(buffer)));

and our program works.

Traditionally you can check full code with test on my github

GitHub - gustawdaniel/codingame-computational-complexity

Contribute to gustawdaniel/codingame-computational-complexity development by creating an account on GitHub.

GitHubgustawdaniel